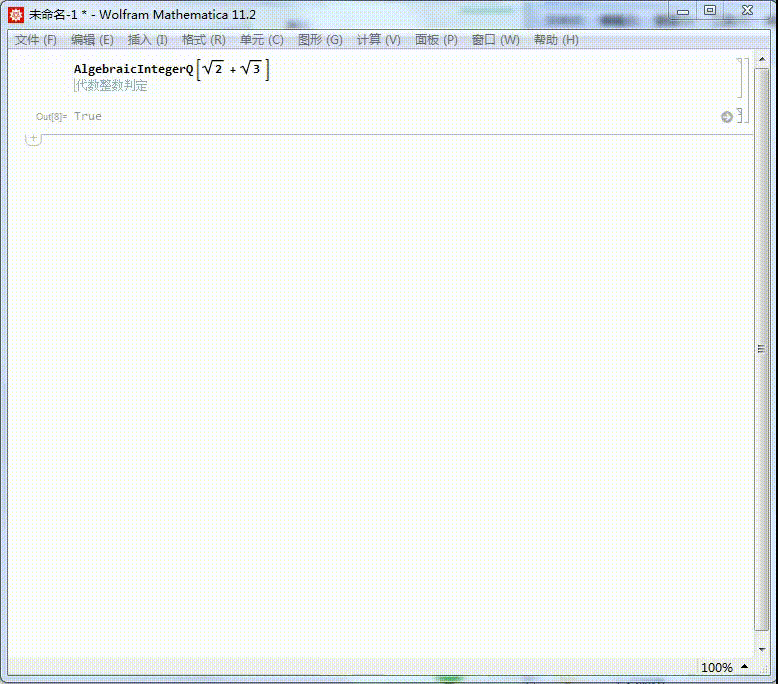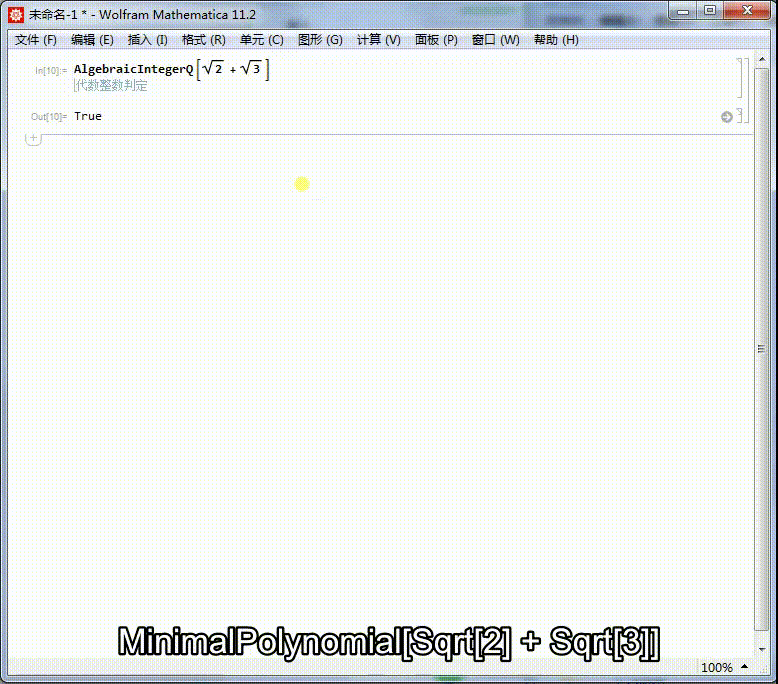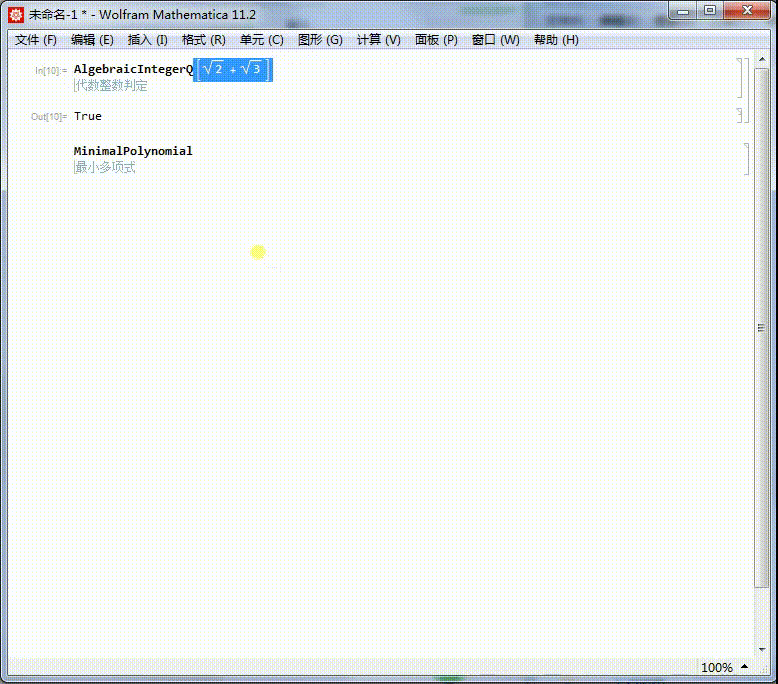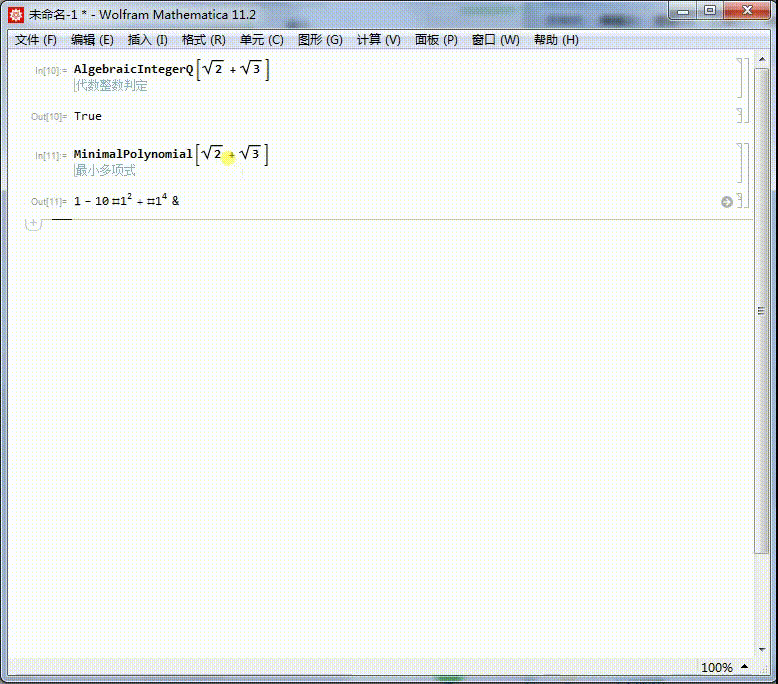
1、我们知道Sqrt[2] + Sqrt[3] 是代数整数,它的本原多项式是:MinimalPolynomial[Sqrt[2] + Sqrt[3]]
3、同样的,Sqrt[2] + Sqrt[3] + Sqrt[5]的本原多项式也可以求出来,结果得到的多项式有点复杂:MinimalPolynomial[Sqrt[2柯计瓤绘] + Sqrt[3] + Sqrt[5],x]

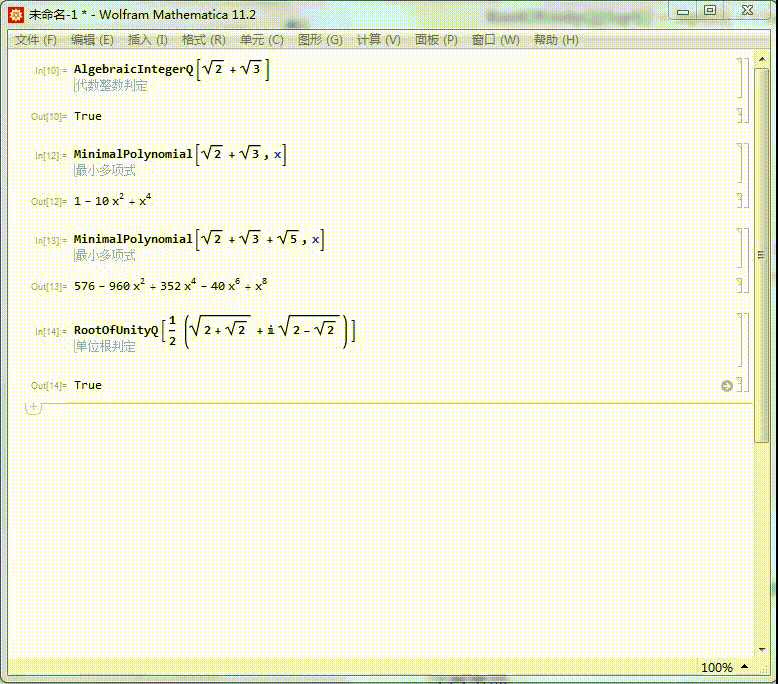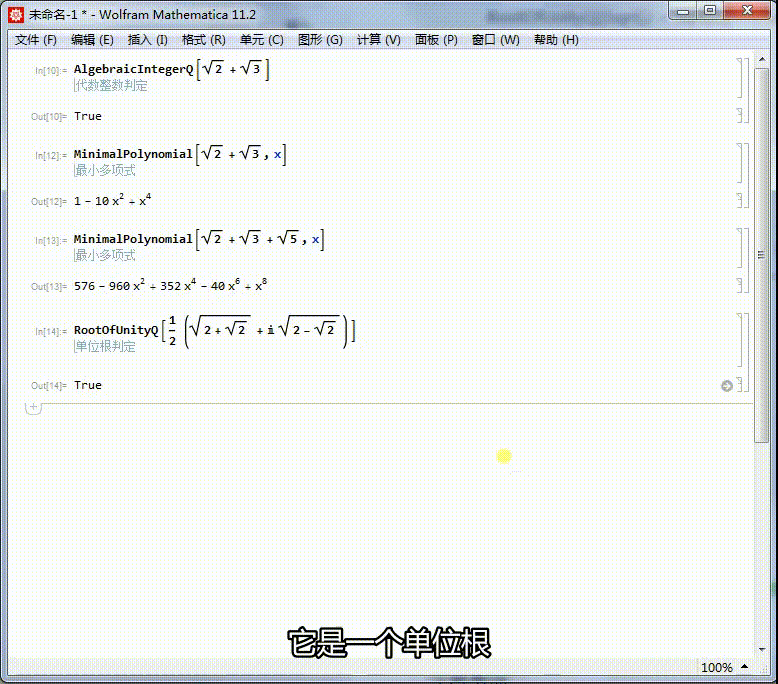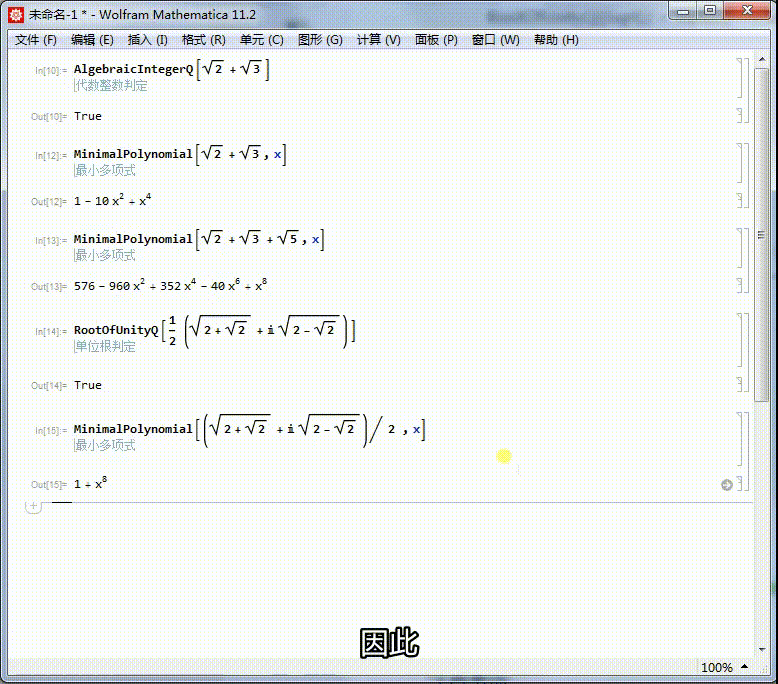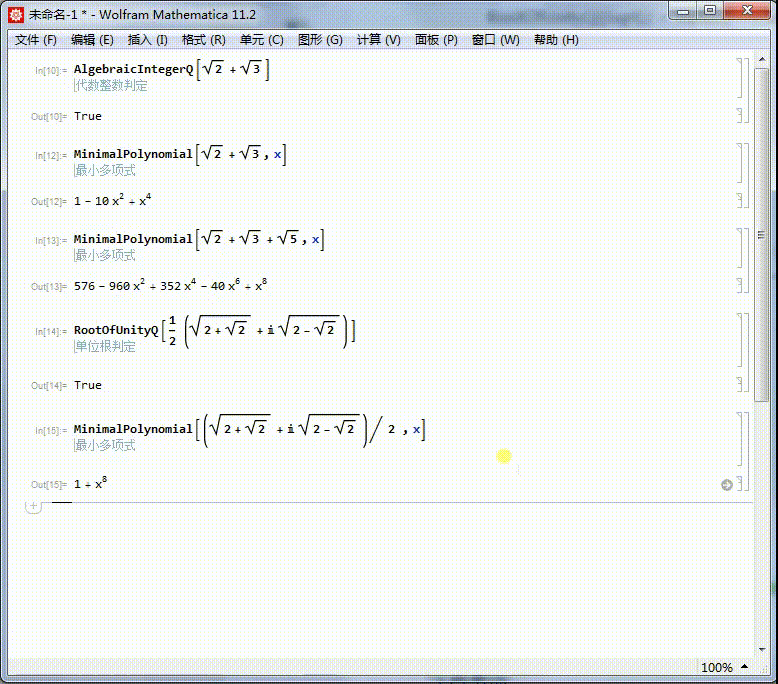
5、求出它的本原多项式,可以进一步证明,它是一个单位根。它的本原方程是x^8+1=0,因此,它是一个16次单位根。
时间:2024-10-16 07:25:19
1、我们知道Sqrt[2] + Sqrt[3] 是代数整数,它的本原多项式是:MinimalPolynomial[Sqrt[2] + Sqrt[3]]

3、同样的,Sqrt[2] + Sqrt[3] + Sqrt[5]的本原多项式也可以求出来,结果得到的多项式有点复杂:MinimalPolynomial[Sqrt[2柯计瓤绘] + Sqrt[3] + Sqrt[5],x]

5、求出它的本原多项式,可以进一步证明,它是一个单位根。它的本原方程是x^8+1=0,因此,它是一个16次单位根。

