定义辅助函数G(x,y)=(x,F(x,y)),我们可以得到G的雅可比矩阵为1 Fx0 Fy其雅可比行列式为Fy。由反挣窝酵聒函数定理知G存在局部的反函数g,定义f(x)=g(x,0)即得隐函数。隐函数的求导公式可以由链式法则得到。
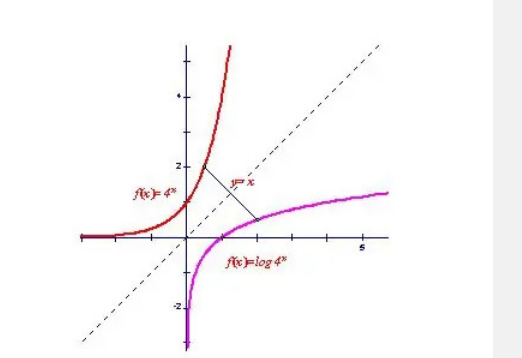
反函数是对一个定函数做逆运算的函数。
一般来说,设函数y=f(x)(x∈A)的值域是C,若找得到一个函数g(y)在每一处g(y)都等于x,这样的函数x= g(y)(y∈C)叫做函数y=f(x)(x∈A)的反函数,记作y=f^(-1)(x) ,反函数x=f^(-1)(y)的定义域、值域分别是函数y=f(x)的值域、定义域。最具代表性的反函数是对数函数与指数函数。
