三角形面积求解问题,是小学、初中、高中乃至大学都一直涉及的考题。本篇经验介绍三种求三角形面积的方法。
2、作高法有时需要作延长线,在小学阶段,学生常常容易由于作了延长线,而弄错底边边长,进而导致计算得到的面积结果不正确。

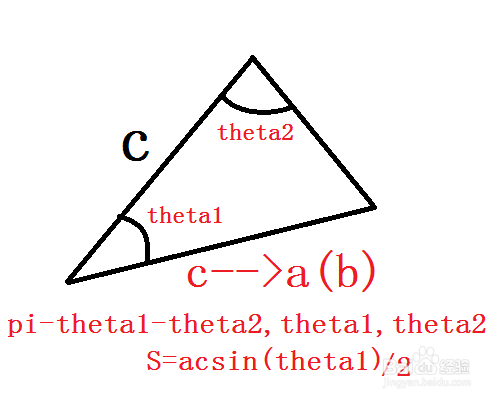
2、实际上,由于正弦定理的形式是丰富的,题目不会轻易地将这种方法的基础条件(如a、b、theta值)告诉答题者,所以解题比较拐弯抹角。例如只给出一边两角,这时还需要依靠余弦定理。
时间:2024-10-17 04:48:01
三角形面积求解问题,是小学、初中、高中乃至大学都一直涉及的考题。本篇经验介绍三种求三角形面积的方法。

2、作高法有时需要作延长线,在小学阶段,学生常常容易由于作了延长线,而弄错底边边长,进而导致计算得到的面积结果不正确。

2、实际上,由于正弦定理的形式是丰富的,题目不会轻易地将这种方法的基础条件(如a、b、theta值)告诉答题者,所以解题比较拐弯抹角。例如只给出一边两角,这时还需要依靠余弦定理。

